| http://www.bymath.net
Прямая
Общее уравнение прямой. Нормальный вектор.
Уравнение прямой с угловым коэффициентом.
Уравнение прямой в
отрезках на осях. Уравнение прямой, проходящей
через две
различные точки. Параметрическое уравнение прямой.
Условие
параллельности прямых. Условие перпендикулярности прямых.
Расстояние между двумя точками. Расстояние от точки до прямой.
Расстояние между параллельными прямыми. Угол
между прямыми.
Общее уравнение прямой:
Ах + Ву + С =
0
,
где А и В не равны нулю
одновременно.
Коэффициенты А и В являются
координатами нормального вектора прямой (
т.е. вектора, перпендикулярного прямой
). При А
=
0 прямая параллельна оси ОХ
, при В
=
0 прямая параллельна оси ОY
.
При В
 0
получаем
уравнение прямой с угловым коэффициентом:
0
получаем
уравнение прямой с угловым коэффициентом:
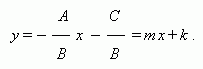
Уравнение прямой, проходящей через точку (
х0
,
у 0
) и не параллельной оси
OY,
имеет вид:
у
– у 0 =
m
( x
– х0 ) ,
где m
–
угловой коэффициент,
равный тангенсу угла, образованного данной прямой и положительным направлением оси ОХ
.
При А
 0,
В
0,
В  0 и
С
0 и
С  0
получаем
уравнение
прямой в отрезках на осях:
0
получаем
уравнение
прямой в отрезках на осях:
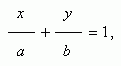
где
a
= –
C
/ A
, b
= – C
/ B
. Эта прямая проходит через точки (
a,
0 )
и (
0,
b
), т.е. отсекает на осях координат отрезки длиной a
и b
.
Уравнение
прямой,
проходящей
через две различные точки
(
х1,
у
1
) и (
х2,
у
2
):
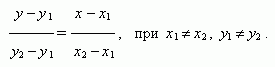
Параметрическое уравнение прямой,
проходящей
через
точку
(
х0
,
у 0
)
и
параллельной
направляющему вектору прямой (
a,
b
)
:
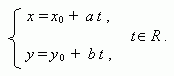
Условие параллельности прямых:
1) для прямых Ах+ Ву+ С = 0 и
Dх+
Eу+
F
= 0 :
AE
–
BD
= 0 ,
2) для прямых у =
m
x+
k
и у =
p
x+
q
: m
=
p
.
Условие перпендикулярности прямых:
1) для прямых Ах+ Ву+ С = 0 и
Dх+
Eу+
F
= 0 :
AD
+
BE
= 0 ,
2) для прямых у =
m
x+
k
и у =
p
x+
q
: m
p
=
– 1 .
Расстояние между двумя точками (
x1, y
1
) и (
x2
, y2
) :
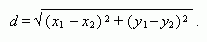
Расстояние от точки
(
х0
,
у
0
) до прямой
Ах+ Ву+ С = 0 :
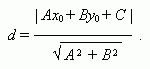
Расстояние между
параллельными прямыми
Ах+ Ву+
С
=
0
и
Dх+
Eу+
F
=
0 :
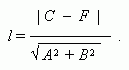
Угол
 между прямыми: между прямыми:
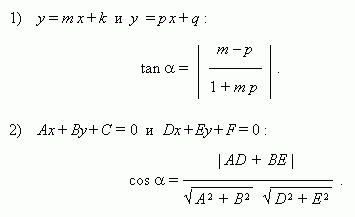
Источник: http://www.bymath.net |