Характеристики случайных величин
Математическое ожидание.
Свойства математического ожидания.
Дисперсия. Свойства дисперсии.
Среднее квадратичное отклонение.
Математическим ожиданием
дискретной случайной величины
Х
, принимающей конечное число значений
хi
с вероятностями рi
, называется сумма:
М
(
Х
) = х1 ·
р1
+ х2 ·
р2 + х3
·
р3 + ... + хn·
рn
.
Свойства математического ожидания:
1) М
(
с
·
Х
) = с
· М
(
Х
) , c
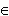 R
,
R
,
2) М
(
Х
+ Y
) = М
(
Х
) + М
(
Y
) , Х
,
Y
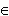 Е ,
Е ,
3)
М
(
Х
· Y
) = М
(
Х
) ·
М
(
Y
) для независимых случайных величин
Х
и
Y
.
Дисперсией
случайной величины
Х
называется число:
D
(
Х
) = М{
[
Х
– М
(
Х
)] 2
}= М
(
Х
2
) – [М
(
Х
)] 2
.
Свойства дисперсии:
1)
D
(
с
·
Х
) = с 2
·
D
(
Х
) , c
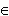 R
,
R
,
2)
D
(
Х
+ Y
) =
D
(
Х
) + D
(
Y
) для независимых случайных величин
Х
и
Y
.
Среднее
квадратичное отклонение:
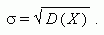
Источник: http://www.bymath.net |