Выпуклость, вогнутость и точки перегиба функции

Вторая производная. Выпуклая и вогнутая функция.

 Достаточное условие вогнутости ( выпуклости ) функции.

Точка перегиба.

Вторая производная. Если производная  f ' ( x ) функции  f ( x ) дифференцируема в точке ( x₀ ), то её производная называется второй производной функции  f ( x )  в точке ( x₀ ), и обозначается  f '' ( x₀ ).  

Функция  f ( x ) называется  выпуклой  на интервале ( a, b ), если её график на этом интервале лежит  ниже  касательной, проведенной к кривой  y = f ( x ) в любой точке ( x₀ ,  f ( x₀ ) ),  x₀ 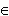( a, b ).

Функция  f ( x ) называется  вогнутой на интервале ( a, b ), если её график на этом интервале лежит  выше  касательной, проведенной к кривой  y = f ( x ) в любой точке ( x₀ ,  f ( x₀ ) ),  x₀ 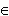( a, b ).

Достаточное условие вогнутости ( выпуклости ) функции.

Пусть функция f ( x ) дважды дифференцируема ( имеет вторую производную ) на интервале ( a, b ), тогда:

если  f '' ( x ) > 0 для любого x 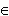( a, b ), то функция  f ( x ) является вогнутой на интервале ( a, b );

если  f '' ( x ) < 0 для любого x 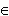( a, b ), то функция  f ( x ) является выпуклой на интервале ( a, b ) .

Точка, при переходе через которую функция меняет выпуклость на вогнутость или наоборот, называется точкой перегиба. Отсюда следует, что если в точке перегиба  x₀  существует вторая производная  f '' ( x₀ ), то  f '' ( x₀ ) = 0.

П р и м е р .

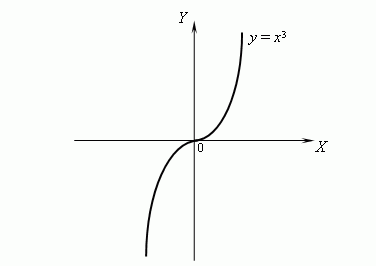
Рассмотрим график функции  y = x3 : Эта функция является вогнутой при  x > 0  и выпуклой при  x < 0. В самом деле,  y'' = 6x, но 6x > 0 при  x > 0  и  6x < 0  при  x < 0, следовательно,  y'' > 0 при x > 0 и  y'' < 0 при x < 0, откуда следует, что функция  y = x3 является вогнутой при  x > 0 и выпуклой при x < 0. Тогда  x = 0 является точкой перегиба функции  y = x3.