Многоугольник
Многоугольник. Вершины, углы,
стороны и диагонали
многоугольника. Периметр
многоугольника.
Простой
многоугольник. Выпуклый многоугольник.
Сумма
внутренних углов выпуклого многоугольника.
Плоская фигура, образованная замкнутой
цепочкой отрезков, называется
многоугольником.
В зависимости от количества
углов многоугольник может быть треугольником, четырёхугольником,
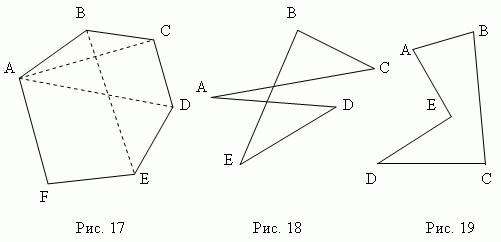
пятиугольником, шестиугольником и т.д. На рис.17 показан
шестиугольник ABCDEF.
Точки А,
В,
C, D,
E, F –
вершины
многоугольника;
углы  A , A ,
 B , B ,  C ,
C ,  D, D,
 E , E ,  F – углы многоугольника;
отрезки AC,
AD,
BE
и т.д. - диагонали;
AB,
BC,
CD,
DE,
EF,
FA
– стороны многоугольника;
сумма длин сторон AB
+ BC
+ … + FA
называется периметром
и обозначается
p
(иногда обозначают – 2p,
тогда p
–
полупериметр).
В
элементарной
геометрии
рассматриваются
только простые
многоугольники, контуры которых не имеют самопересечений, как показано
на рис.18. Если все диагонали лежат внутри многоугольника, он называется
выпуклым. Шестиугольник на рис.17 выпуклый; пятиугольник ABCDE
на рис.19 не выпуклый, так как его диагональ
AD
лежит
снаружи. Сумма внутренних углов выпуклого многоугольника равна 180º (
n
– 2 ), где n
- число углов (или сторон) многоугольника.
F – углы многоугольника;
отрезки AC,
AD,
BE
и т.д. - диагонали;
AB,
BC,
CD,
DE,
EF,
FA
– стороны многоугольника;
сумма длин сторон AB
+ BC
+ … + FA
называется периметром
и обозначается
p
(иногда обозначают – 2p,
тогда p
–
полупериметр).
В
элементарной
геометрии
рассматриваются
только простые
многоугольники, контуры которых не имеют самопересечений, как показано
на рис.18. Если все диагонали лежат внутри многоугольника, он называется
выпуклым. Шестиугольник на рис.17 выпуклый; пятиугольник ABCDE
на рис.19 не выпуклый, так как его диагональ
AD
лежит
снаружи. Сумма внутренних углов выпуклого многоугольника равна 180º (
n
– 2 ), где n
- число углов (или сторон) многоугольника.
Источник: http://www.bymath.net |