Метод интервалов.  Решить неравенство:  ( x – 3 )( x – 5 ) < 2( x – 3 ). Здесь нельзя делить обе части неравенства на ( x – 3 ), так как мы не знаем знака этого двучлена ( он содержит неизвестное x ). Поэтому мы перенесём все члены неравенства в левую часть:

( x – 3 )( x – 5 ) – 2( x – 3 ) < 0 ,

разложим её на множители: 

( x – 3 )( x – 5  – 2 ) < 0 ,

и получим: ( x – 3 )( x – 7 ) < 0. Теперь определим знак произведения в левой части неравенства в различных числовых интервалах. Заметим, что  x = 3  и  x = 7 - корни этого выражения. Поэтому вся числовая ось разделится этими корнями на следующие три интервала:

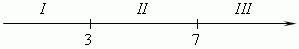
В интервале I ( x < 3 ) оба сомножителя отрицательны, следовательно, их произведение положительно; в интервале II ( 3 < x < 7 ) первый множитель ( x – 3 ) положителен, а второй  ( x – 7 ) отрицателен, поэтому их произведение отрицательно; в интервале III ( x > 7 ) оба сомножителя положительны, следовательно, их произведение также положительно. Теперь остаётся выбрать интервал, в котором наше произведение отрицательно. Это интервал II, следовательно, решение неравенства: 3 < x < 7. Последнее выражение - так называемое двойное неравенство. Оно означает, что  x должен быть одновременно больше 3 и меньше 7.

П р и м е р .  Решить следующее неравенство методом интервалов:

( x – 1 )( x – 2 )( x – 3 ) … ( x –100 ) > 0 .

Р е ш е н и е . Корни левой части неравенства очевидны: 1, 2, 3, …, 100.

                        Они разбивают числовую ось на 101 интервал:

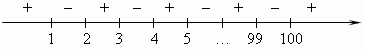
                        Так как количество скобок в левой части чётно (равно 100), то      

                        при  x < 1, когда все множители отрицательны, их произведение 

                        положительно. При переходе через корень происходит смена

                        знака произведения. Поэтому следующим интервалом, внутри

                        которого произведение положительно, будет ( 2, 3 ), затем ( 4, 5 ),

                        затем  ( 6, 7 ), … , ( 98, 99 ) и наконец,  x >100.   

                        Таким образом, данное неравенство имеет решение: 

                        x < 1,  2 < x < 3,  4 < x < 5 ,…,  x >100.

Итак, чтобы решить алгебраическое неравенство, надо перенести все его члены в левую (или правую) часть и решить соответствующее уравнение. После этого найденные корни нанести на числовую ось; в результате она разбивается на некоторое число интервалов. На последнем этапе решения нужно определить, какой знак имеет многочлен внутри каждого из этих интервалов, и выбрать нужные интервалы в соответствии со знаком решаемого неравенства.   

Заметим, что большинство трансцендентных неравенств заменой неизвестного приводятся к алгебраическому неравенству. Его надо решить относительно нового неизвестного, а затем путём обратной замены найти решение для исходного неравенства.

Системы неравенств. Чтобы решить систему неравенств, необходимо решить каждое из них, и совместить их решения. Это совмещение приводит к одному из двух возможных случаев: либо система имеет решение, либо нет.

П р и м е р  1.  Решить систему неравенств:

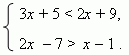
Р е ш е н и е.  Решение первого неравенства:  x < 4 ;  а второго:  x > 6.

                        Таким образом, эта система неравенств не имеет решения.

                        ( Почему ? )

П р и м е р  2.  Решить систему неравенств:

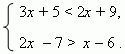
Р е ш е н и е.  Первое неравенство, как и прежде, даёт: x < 4; но решение

                        второго неравенства в данном примере: x > 1.

                        Таким образом, решение системы неравенств: 1 < x < 4.