Неравенства: общие сведения
Неравенство.
Тождественное неравенство.
Строгие и нестрогие
неравенства.
Решение неравенств
и систем неравенств.
Основные свойства
неравенств.
Некоторые важные неравенства.
Два выражения
(числовые или буквенные), соединённые одним из знаков:
«больше» (>), «меньше» (<), «больше или равно»
(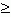 ),
«меньше или равно» ( ),
«меньше или равно» (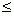 )
образуют
неравенство
(числовое или буквенное). Любое справедливое неравенство
называется тождественным. Например, тождественны
следующие неравенства:
3
· 7 – 20 > 2
· 4
-10,
a²
³ 0,
|
- 5 | >
3. (Почему?). В зависимости от знака неравенства мы имеем либо
строгие неравенства
( >
, < )
,
либо нестрогие ( )
образуют
неравенство
(числовое или буквенное). Любое справедливое неравенство
называется тождественным. Например, тождественны
следующие неравенства:
3
· 7 – 20 > 2
· 4
-10,
a²
³ 0,
|
- 5 | >
3. (Почему?). В зависимости от знака неравенства мы имеем либо
строгие неравенства
( >
, < )
,
либо нестрогие ( 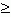 , , 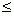 ). Запись 5a ). Запись 5a 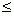 4b
означает, что 5a
либо меньше
4b,
либо равно ему. Буквенные величины, входящие в неравенство,
могут быть как известными, так и неизвестными.
Решить неравенство –
значит найти границы, внутри которых должны
находиться
неизвестные, так чтобы неравенство было справедливым.
Решить
систему неравенств – значит найти границы, внутри которых должны
находиться
неизвестные, так чтобы все неравенства, входящие
в систему, были справедливы одновременно. 4b
означает, что 5a
либо меньше
4b,
либо равно ему. Буквенные величины, входящие в неравенство,
могут быть как известными, так и неизвестными.
Решить неравенство –
значит найти границы, внутри которых должны
находиться
неизвестные, так чтобы неравенство было справедливым.
Решить
систему неравенств – значит найти границы, внутри которых должны
находиться
неизвестные, так чтобы все неравенства, входящие
в систему, были справедливы одновременно.
Основные
свойства неравенств.
| 1. |
Если
a
< b,
то
b
> a
; или если a
> b,
то b
< a
.
|
| 2. |
Если
a > b,
то a
+ c
> b
+ c;
или если a
< b,
то a
+ c
< b
+ c.
То есть, можно
прибавлять (вычитать) одно и то же число к обеим частям
неравенства.
|
| 3. |
Если
a
> b
и
c
> d,
то a
+ c
> b
+ d
. То есть,
неравенства одного
смысла (с одинаковым
знаком > или < ) можно
почленно складывать.
Заметим, что неравенства одного смысла нельзя почленно вычитать
одно
из другого,
так
как результат может быть неверным.
|
| 4. |
Если
a
> b
и
c
< d,
то a
– c
> b
– d
. Или если
a
< b
и
c
> d,
то a – c < b – d .
То есть,
неравенства противоположного
смысла можно почленно вычитать одно из другого, и брать знак неравенства,
являющегося
уменьшаемым.
|
| 5. |
Если a
> b
и
m
> 0, то
ma
> mb
и a/m
> b/m
. То есть, обе части
неравенства можно
умножить или разделить на одно и то же положительное
число. Неравенство при этом сохраняет свой знак.
|
| 6. |
Если
a
> b
и
m
< 0, то
ma
< mb
и a/m
< b/m
. То есть,
обе части неравенства можно
умножить или разделить на одно и то же отрицательное
число. Неравенство при этом меняет свой знак на обратный.
|
Некоторые важные неравенства.
1. | a + b | 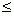 | a | + | b | .
Модуль суммы меньше или равен сумме модулей. | a | + | b | .
Модуль суммы меньше или равен сумме модулей.
2. a + 1 / a 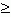 2, ( a –
положительно ). Равенство будет только при a
= 1. 2, ( a –
положительно ). Равенство будет только при a
= 1.
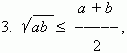 ( a
и
b
–
положительны ). Равенство только при
a
=
b. ( a
и
b
–
положительны ). Равенство только при
a
=
b.
Среднее геометрическое не больше среднего арифметического.
В общем случае это неравенство имеет вид:
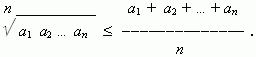
Числа a1
,
a2
,
…,
an
-
положительны. Равенство имеет место, если
только все числа равны.
Источник: http://www.bymath.net |