Плоскость
Общее уравнение плоскости. Нормальный вектор.
Уравнение плоскости
в отрезках на осях.
Уравнение плоскости, проходящей через
заданную
точку и перпендикулярной заданному вектору.
Условие параллельности плоскостей.
Условие перпендикулярности плоскостей.
Расстояние
между двумя точками.
Расстояние от точки до плоскости.
Угол между плоскостями.
Общее уравнение плоскости:
Ах + Ву
+ Сz
+
D
= 0 ,
где А,
B
и
C
не равны нулю одновременно.
Коэффициенты А,
B
и
C
являются координатами нормального вектора
плоскости (
т.е. вектора, перпендикулярного плоскости
).
При А
 0, В
0, В
 0, С
0, С
 0 и
D
0 и
D
 0
получаем
уравнение плоскости
в отрезках на осях:
0
получаем
уравнение плоскости
в отрезках на осях:
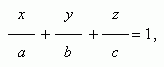
где
a
= –
D
/ A
, b
= – D
/ B,
c
= – D
/ C.
Эта плоскость проходит через точки (
a,
0, 0
), (
0,
b,
0
) и (
0, 0, с
), т.е. отсекает на осях координат
отрезки длиной a,
b
и c
.
Уравнение плоскости,
проходящей через точку ( х0
,
у
0
,
z
0 ) и перпендикулярной
вектору (
А,
В, C
)
:
А
(
х
– х0
)
+ В
( у – у 0
)
+ С
(
z
–
z
0
)
=
0 .
Условие параллельности плоскостей
Ах+ Ву+ Сz+
D
= 0 и
Eх+
Fу+
Gz+ H =
0:
AF
– BE = BG – CF = AG – CE = 0 .
Условие перпендикулярности плоскостей
Ах+ Ву+ Сz+
D
= 0 и
Eх+
Fу+
Gz+
H =
0:
АE+
ВF+
СG
= 0 .
Расстояние
между двумя точками ( х1
,
у
1
,
z
1
)
и
(
x2
,
y2
,
z2)
:
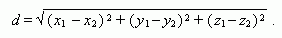
Расстояние
от точки
( х0
,
у
0
,
z
0
)
до
плоскости
Ах
+ Ву
+ Сz
+
D
= 0 :
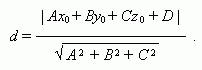
Угол
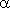 между
плоскостями Ах+ Ву+ Сz+
D
= 0 и
Eх+
Fу+
Gz+
H
=
0: между
плоскостями Ах+ Ву+ Сz+
D
= 0 и
Eх+
Fу+
Gz+
H
=
0:
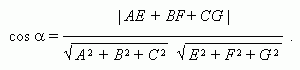
Источник: http://www.bymath.net |