Преобразования
координат
Параллельный
перенос. Гомотетия.
Симметрия. Аффинное преобразование.
Рассмотрим ряд преобразований, связанных с
переходом из одной системы координат в другую. Здесь ( х,
у
,
z
) и ( х',
у',
z'
) - координаты произвольной точки
Р соответственно в старой и новой системе координат.
Параллельный перенос.
Передвинем систему координат
X
Y
Z
в трёхмерном пространстве так, чтобы оси
OX,
OY
и OZ
оставались параллельны самим себе, а
начало координат О сместилось в точку О' (
a,
b,
с
).
Получим новую систему координат
X'
Y'
Z'
.
Координаты
точки Р в новой и старой системе координат связаны соотношениями:
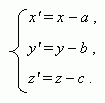
Гомотетия с
центром
О (
a
,
b
,
c
) и
коэффициентом
k
 0 :
0 :
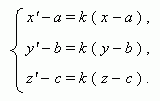
Симметрия
относительно плоскости
XOY
:
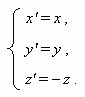
Аффинное
преобразование:
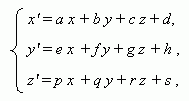

Источник: http://www.bymath.net |