Гипербола

Гипербола. Фокусы. Уравнение гиперболы. Фокусное расстояние.

Действительная и мнимая оси гиперболы. Эксцентриситет.

Асимптоты гиперболы. Уравнение касательной к гиперболе.

Условие касания прямой и гиперболы.

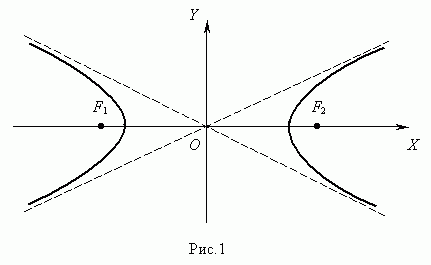
Гиперболой ( рис.1 ) называется геометрическое место точек, модуль разности расстояний от которых до двух заданных точек  F₁ и F₂ , называемых  фокусами гиперболы, есть величина постоянная.

Уравнение гиперболы ( рис.1 ) :

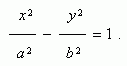
Здесь начало координат является центром симметрии гиперболы, а оси координат – её осями симметрии.

Отрезок  F₁F₂ = 2 с ,  где 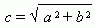, называется фокусным расстоянием. Отрезок  AB = 2 a называется  действительной осью гиперболы, а отрезок  CD = 2 b –  мнимой осью гиперболы. Число  e = c / a ,  e > 1 называется эксцентриситетом гиперболы. Прямые   y = ± ( b / a ) x  называются асимптотами гиперболы.

Пусть  Р ( х₁ ,  у ₁ ) – точка гиперболы, тогда  уравнение касательной к гиперболе в данной точке имеет вид:

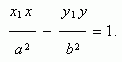
Условие касания прямой  y = m x + k  и гиперболы  х ² / a ²  –  у  ² / b ²  = 1 :

k ²  = m ² a ² – b ² .