Основные понятия. Примеры множеств

Множество. Элемент множества. Конечное множество.

Пустое множество. Бесконечное множество. Счётное множество.

Несчётное множество. Выпуклое множество. Способы задания множеств.

Множество и элемент множества относятся к числу первичных понятий, для которых не существует определений в строгом смысле слова. Поэтому обычно говорят о множестве как о наборе предметов ( элементов множества ), наделённых определёнными общими свойствами. Множество книг в библиотеке, множество автомобилей на стоянке, множество звёзд на небосводе, растительный и животный мир Земли – всё это примеры множеств.

Конечное множество состоит из конечного числа элементов, например, множество страниц в книге, множество учеников в школе и т.д.

Пустое множество ( 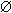) не содержит ни одного элемента, например, множество крылатых слонов, множество корней уравнения  sin x = 2  и т.д.

Бесконечное множество состоит из бесконечного числа элементов, т.е. это множество, которое не является ни конечным, ни пустым. Примеры: множество действительных чисел, множество точек плоскости, множество атомов во Вселенной и т.д.

Счётное множество – множество, элементы которого можно пронумеровать. Например, множества натуральных, чётных, нечётных чисел. Счётное множество может быть конечным ( множество книг в библиотеке ) или бесконечным ( множество целых чисел, его элементы можно пронумеровать следующим образом:

элементы множества:    …, –5,   – 4,   –3,   –2,   –1,   0,   1,   2,   3,   4,   5, …

номера элементов:           ...   11       9      7      5      3    1    2    4    6    8   10 ...  ) .

Несчётное множество – множество, элементы которого невозможно пронумеровать. Например, множество действительных чисел. Несчётное множество может быть только бесконечным ( продумайте, почему ? ).

Выпуклое  множество – множество, которое наряду с любыми двумя точками А и В содержит также весь отрезок  АВ. Примеры выпуклых множеств: прямая, плоскость, круг. Однако, окружность не является выпуклым множеством.

Способы задания множеств. Множество может быть задано следующим образом:

– перечислением всех его элементов по их названиям ( так описываются множество книг в библиотеке, множество учеников в классе, алфавит любого языка и т.д.);

– заданием общей характеристики ( общих свойств ) элементов данного множества ( например, множество рациональных чисел, собаки, семейство кошачих и т.д.);

– формальным законом построения элементов множества ( например, формула общего члена числовой последовательности, Периодическая система элементов Менделеева и т.д.).