8.

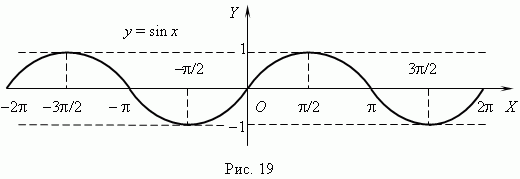
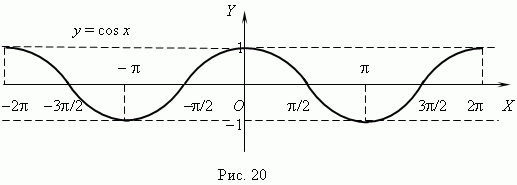
Тригонометрические функции. При построении тригонометрических функций мы используем радианную меру измерения углов. Тогда функция  y = sin x представляется графиком ( рис.19 ). Эта кривая называется синусоидой.   График функции  y = cos x представлен на рис.20; это также синусоида, полученная в результате перемещения графика  y = sin x  вдоль оси Х  влево на /2. Из этих графиков очевидны характеристики и свойства этих функций: - область определения: - 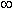< x < + 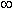; область значений:  -1   y +1;     - эти функции периодические: их период 2 ; - функции ограниченные  ( | y | 1 ), всюду непрерывные, не монотонные, но     имеющие так называемые интервалы монотонности, внутри которых они      ведут себя, как монотонные функции ( см. графики рис.19 и рис.20 ); - функции имеют бесчисленное множество нулей ( подробнее см. раздел     «Тригонометрические уравнения» ).   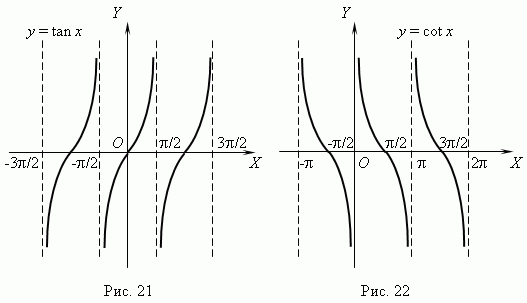Графики функций  y = tan x  и  y = cot x  показаны соответственно на рис.21 и рис.22             Из графиков видно, что эти функции: периодические ( их период ),       неограниченные, в целом не монотонные, но имеют интервалы монотонности       ( какие? ), разрывные ( какие точки разрыва имеют эти функции? ). Область             определения и область значений этих функций:

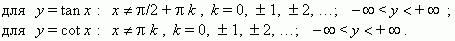9.

Обратные тригонометрические функции. Определения обратных   тригонометрических функций и их основные свойства приведены в  одноимённом разделе в главе «Тригонометрия». Поэтому здесь мы ограничимся  лишь короткими комметариями, касающимися их графиков, полученных   поворотом графиков тригонометрических функций вокруг биссектрисы 1-го  координатного угла.

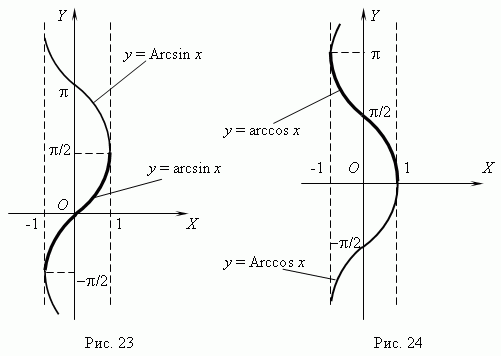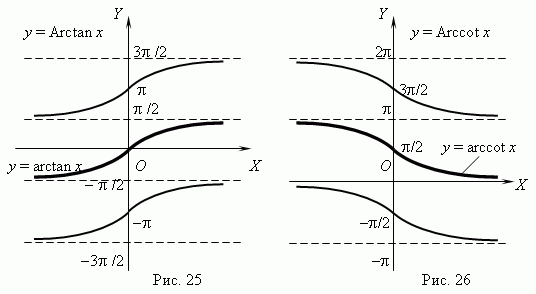
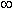Функции  y = Arcsin x ( рис.23 ) и  y = Arccos x ( рис.24 ) многозначные, неограниченные; их область определения и область значений соответственно:  -1   x +1  и - < y < + 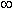. Поскольку эти функции многозначные, не

рассматриваемые в элементарной математике, в качестве обратных тригонометрических функций рассматриваются их главные значения:  y = arcsin x  и   y = arccos x; их графики выделены на рис.23 и рис.24 жирными линиями.

Функции  y = arcsin x  и  y = arccos x обладают следующими характеристиками и свойствами:

- у обеих функций одна и та же область определения:  -1   x +1 ;

  их области значений:  -/2   y /2  для  y = arcsin x  и  0   y для  y = arccos x;

- функции ограниченные, непериодические, непрерывные и монотонные

   ( y = arcsin x – возрастающая функция;  y = arccos x – убывающая );

- каждая функция имеет по одному нулю ( x = 0  у функции  y = arcsin x и

   x = 1  у функции  y = arccos x).

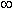
Функции  y = Arctan x ( рис.25 ) и  y = Arccot x ( рис.26 ) - многозначные, неограниченные функции; их область определения: - x + 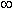. Их главные значения  y = arctan x  и  y = arccot x рассматриваются в качестве обратных тригонометрических функций; их графики выделены на рис.25 и рис.26 жирными ветвями.

Функции  y = arctan x и  y = arccot x имеют следующие характеристики и свойства:

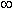
- у обеих функций одна и та же область определения:  - x + ;

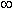  их области значений:  -/2 < y < /2  для  y = arctan x  и  0 < y <   для  y = arccos x;

- функции ограниченные, непериодические, непрерывные и монотонные

  ( y = arctan x – возрастающая функция;  y = arccot x – убывающая );

- только функция  y = arctan x имеет единственный ноль ( x = 0 );

  функция  y = arccot x нулей не имеет.