Элементарные функции и их графики
Прямая
пропорциональность. Линейная
функция.
Обратная пропорциональность.
Гипербола.
Квадратичная функция.
Квадратная парабола.
Степенная функция.
Показательная функция.
Логарифмическая функция.
Тригонометрические функции.
Обратные тригонометрические функции.
| 1. |
Пропорциональные величины.
Если
переменные
y
и
x
прямо
пропорциональны,
то функциональная
зависимость между ними выражается уравнением:
y = k x ,
где
k
- постоянная величина ( коэффициент пропорциональности ).
График
прямой
пропорциональности
–
прямая линия,
проходящая
через
начало
координат
и
образующая с
осью
X
угол
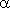 ,
тангенс
которого
равен
k
:
tan ,
тангенс
которого
равен
k
:
tan
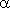 = k (
рис.8
).
Поэтому,
коэффициент
пропорциональности
называется
также
угловым
коэффициентом.
На рис.8 показаны три графика для
k
= 1/3,
k
= 1 и
k
= -3
.
= k (
рис.8
).
Поэтому,
коэффициент
пропорциональности
называется
также
угловым
коэффициентом.
На рис.8 показаны три графика для
k
= 1/3,
k
= 1 и
k
= -3
.
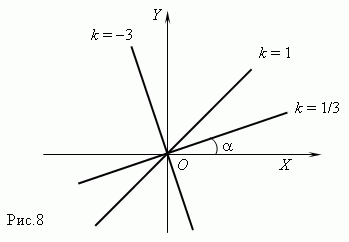
|
| 2. |
Линейная функция.
Если
переменные
y
и x
связаны уравнением
1-ой степени:
A x + B y
= C ,
где по крайней мере одно из чисел
A
или
B
не
равно нулю,
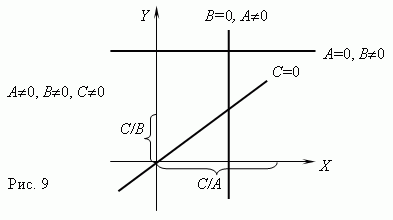
то графиком этой функциональной
зависимости является прямая линия. Если
C
= 0, то
она проходит через начало
координат, в противном случае - нет. Графики линейных
функций для различных комбинаций
A,
B,
C
показаны на рис.9.
|
| 3. |
Обратная
пропорциональность.
Если
переменные
y
и
x
обратно
пропорциональны,
то
функциональная зависимость
между ними выражается
уравнением:
y
= k / x ,
где
k
- постоянная величина.
График
обратной пропорциональности
–
гипербола
(
рис.10
).
У
этой
кривой
две ветви.
Гиперболы
получаются при пересечении
кругового конуса
плоскостью
(
о
конических сечениях см.
раздел «Конус» в главе
«Стереометрия»
). Как показано на рис.10,
произведение координат точек гиперболы
есть
величина
постоянная,
в нашем примере равная
1.
В
общем случае
эта величина равна
k,
что
следует из
уравнения гиперболы: xy
=
k.
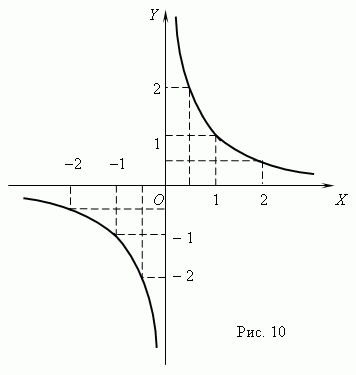
Основные характеристики и свойства
гиперболы:
- область определения
функции: x
 0,
область значений:
y
0,
область значений:
y
 0 ;
0 ;
- функция монотонная (
убывающая
) при
x
< 0 и при x
> 0, но не
монотонная в целом из-за точки
разрыва x
= 0 (
подумайте, почему ?
);
- функция
неограниченная,
разрывная в точке
x
= 0,
нечётная,
непериодическая;
-
нулей функция не имеет.
|
| 4. |
Квадратичная функция.
Это функция:
y
= ax
2
+ bx
+ c,
где a,
b,
c
-
постоянные, a
 0.
В простейшем случае имеем: b
=
c
= 0 и
y
= ax
2.
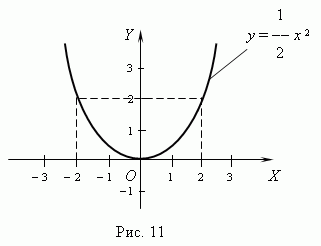
График этой функции квадратная парабола - кривая, проходящая через
начало координат (
рис.11
).
Каждая парабола имеет
ось
симметрии
OY,
которая называется осью параболы.
Точка
O
пересечения параболы с её осью
называется вершиной
параболы.
0.
В простейшем случае имеем: b
=
c
= 0 и
y
= ax
2.
График этой функции квадратная парабола - кривая, проходящая через
начало координат (
рис.11
).
Каждая парабола имеет
ось
симметрии
OY,
которая называется осью параболы.
Точка
O
пересечения параболы с её осью
называется вершиной
параболы.
График
функции
y
= ax
2
+ bx
+ c
- тоже квадратная парабола того
же вида, что
и
y
= ax
2,
но
её
вершина лежит
не в
начале
координат,
а в
точке
с
координатами:
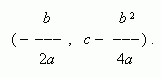
Форма и расположение квадратной
параболы в системе координат полностью зависит от двух параметров:
коэффициента a
при
x2
и дискриминанта D: D
=
b2
–
4ac.
Эти свойства следуют из
анализа корней квадратного уравнения (см.
соответствующий раздел в
главе «Алгебра»). Все возможные различные
случаи для квадратной параболы показаны на рис.12.
|
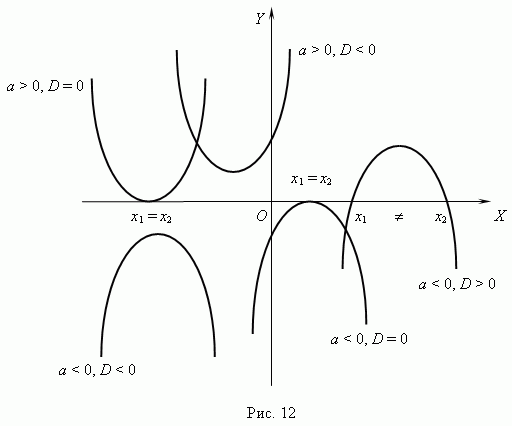
Изобразите, пожалуйста, квадратную
параболу для случая a
> 0, D
> 0 .
Основные характеристики и свойства
квадратной параболы:
- область определения функции:
-
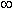 <
x
< +
<
x
< +
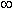 (
т.e.
x
(
т.e.
x
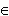 R ), а область
R ), а область
значений:
… ( ответьте, пожалуйста , на этот вопрос сами !
);
- функция в целом не монотонна, но
справа или слева от вершины
ведёт себя, как монотонная;
- функция неограниченная, всюду
непрерывная, чётная при b
= c
= 0,
и
непериодическая;
-
при
D
< 0
не имеет нулей. ( А что при D
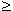 0 ? ) . 0 ? ) .
Источник: http://www.bymath.net |