Основные понятия и свойства функций

Область определения и область значений функции.

Правило (закон) соответствия. Монотонная функция.

Ограниченная и неограниченная функции. Непрерывная и

разрывная функции. Чётная и нечётная функции.

Периодическая функция. Период функции.

Нули функции. Асимптота.

Область определения и область значений функции. В элементарной математике изучаются функции только на множестве действительных чисел R. Это значит, что аргумент функции может принимать только те действительные значения, при которых функция определена, т.e. она также принимает только действительные значения. Множество X всех допустимых действительных значений аргумента  x, при которых функция  y = f ( x ) определена, называется областью определения функции. Множество Y всех действительных значений  y, которые принимает функция, называется областью значений функции. Теперь можно дать более точное определение функции: правило (закон) соответствия между множествами  X  и Y, по которому для каждого элемента из множества X можно найти один и только один элемент из множества Y, называется функцией.

Из этого определения следует, что функция считается заданной, если:

      - задана область определения функции X ;

      - задана область значений функции Y ;

- известно правило ( закон ) соответствия, причём такое, что для каждого    

   значения аргумента может быть найдено только одно значение функции.

Это требование однозначности функции является обязательным.

Монотонная функция. Если для любых двух значений аргумента  x₁  и  x₂ из условия  x₂ > x₁ следует  f ( x₂ ) > f ( x₁ ), то функция  f ( x ) называется возрастающей; если для любых  x₁  и  x₂  из условия  x₂ > x₁ следует  f ( x₂ ) < f ( x₁ ), то функция  f ( x ) называется убывающей. Функция, которая только возрастает или только убывает, называется монотонной.

Ограниченная и неограниченная функции. Функция называется  ограниченной, если существует такое положительное число M, что |  f ( x ) |  M  для всех значений  x . Если такого числа не существует, то функция - неограниченная.

П р и м е р ы .

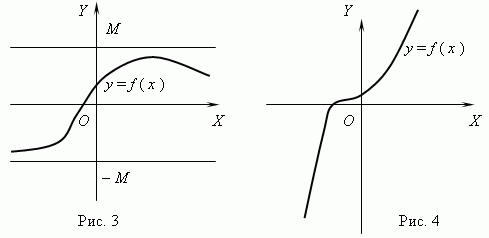
Функция, изображённая на рис.3, является ограниченной, но не монотонной. Функция на рис.4 - как раз наоборот, монотонная, но неограниченная. ( Объясните это, пожалуйста ! ).

Непрерывная и разрывная функции. Функция  y = f ( x ) называется непрерывной в точке  x = a, если :

 1)  функция определена при  x = a,  т.e.  f ( a ) существует;

 2)  существует конечный предел  lim  f ( x ) ;

                                                         x→a

      ( см. раздел «Пределы функций» в главе «Основы анализа» )

 3)   f ( a ) = lim  f ( x ) .

                         x→a 

Если не выполняется хотя бы одно из этих условий, то функция называется разрывной в точке  x = a. 

Если функция непрерывна во всех точках своей области определения, то она называется непрерывной функцией.