Тригонометрические неравенства
При решении тригонометрических неравенств мы используем свойства
неравенств, известные из алгебры, а также различные тригонометрические
преобразования и формулы. Использование единичного круга при решении
тригонометрических неравенств почти необходимо. Рассмотрим ряд примеров.
П р и м е р 1 . Решить неравенство: sin x
> 0.
Р е ш е н и е . В пределах одного оборота единичного радиуса
это неравенство
справедливо при 0 < x <
 .
Теперь необходимо добавить период .
Теперь необходимо добавить период
синуса 2 n :
n :
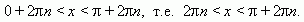
П р и м е р 2 . Решить неравенство: sin x
> 0.5 .
Р е ш е н и е .
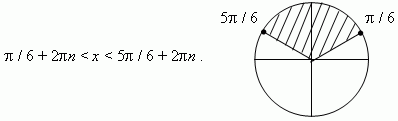
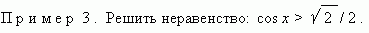
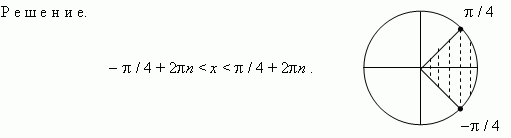
П р и м
е р 4 . Решить систему неравенств:
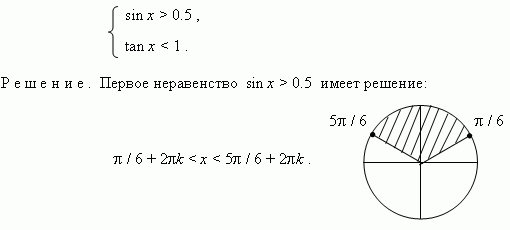
Второе
неравенство
tan
x
< 1 имеет решение:
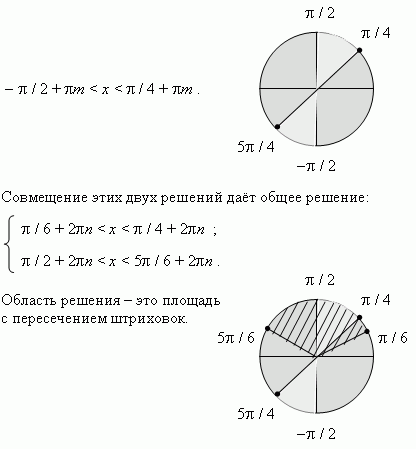
Источник: http://www.bymath.net |