Тригонометрические функции острого угла

Тригонометрические функции острого угла:

синус, косинус, тангенс, котангенс, секанс, косеканс.
Точные значения тригонометрических функций

для некоторых часто используемых острых углов.

Тригонометрические функции острого угла есть отношения различных пар сторон прямоугольного треугольника   ( рис.2 ):

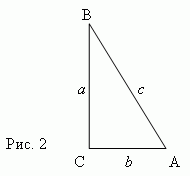
1) Синус - отношение противолежащего катета к гипотенузе:  sin A = a / c .  

2) Косинус - отношение прилежащего катета к гипотенузе:  cos A = b / c .

3) Тангенс - отношение противолежащего катета к прилежащему:  tan A = a / b .

4) Котангенс - отношение прилежащего катета к противолежащему: cot A = b / a .

5) Секанс - отношение гипотенузы к прилежащему катету:  sec A = c / b .

6) Косеканс - отношение гипотенузы к противолежащему катету: cosec A = c / a .

Аналогично записываются формулы для другого острого угла B ( Запишите их, пожалуйста ! ).

П р и м е р .   Прямоугольный треугольник ABC  ( рис.2 ) имеет катеты:

                         a = 4,  b = 3. Найти синус, косинус и тангенс угла A.

Р е ш е н и е .  Во-первых, найдём гипотенузу, используя теорему Пифагора:

                                                      c ² = a ² + b ² ,

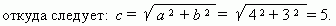
                         Согласно вышеприведенным формулам имеем:

                         sin A = a / c = 4 / 5;  cos A = b / c = 3 / 5;  tan A = a / b = 4 / 3. 

Для некоторых углов можно записать точные значения их тригонометрических функций. Наиболее важные случаи приведены в таблице:

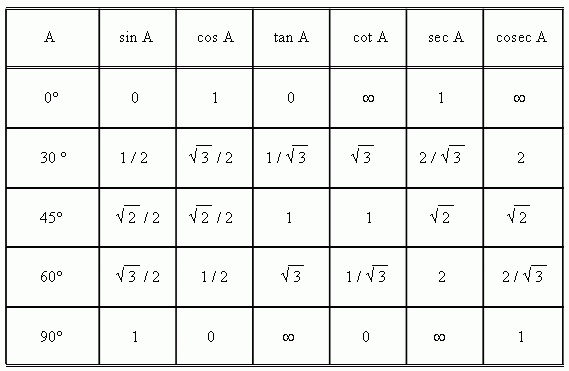
Углы 0° и 90°, строго говоря, не являются острыми в прямоугольном треугольнике, однако при расширении понятия тригонометрических функций ( см. далее ) эти углы также рассматриваются. Символ 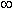  в таблице означает, что абсолютное значение функции неограниченно возрастает, если угол приближается к указанному значению.