Математическая индукция

    Пусть требуется доказать некоторое свойство ( это может быть формула, тождество, неравенство, утверждение и т.д.), зависящее от натурального числа  n. Если:

    1)  это свойство имеет место для некоторого натурального числа  n₀ ,

    2)  из условия справедливости этого свойства  при  n = k  следует его

         справедливость при  n = k + 1  для любого  k 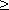n₀ ,

    то тогда это свойство имеет место для любого натурального  n 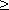n₀ .

    П р и м е р .   Доказать, что  1 + 3 + 5 + ... + ( 2n – 1 ) = n ² .

                           Для доказательства применим метод математической индукции.

                           Очевидно, что при  n = 1 данное равенство справедливо. Предположим,

                           что оно справедливо при некотором  k , т.е. имеет место

                                                              1 + 3 + 5 + ... + ( 2k – 1 ) = k ² .

                           Докажем, что тогда оно имеет место и при  k + 1 . Рассмотрим

                           соответствующую сумму при  n = k + 1 :

                           1 + 3 + 5 + ... + ( 2k – 1 ) + ( 2k + 1 ) = k ² + ( 2k + 1 ) = ( k  + 1 ) ² .

                           Таким образом, из условия, что это равенство справедливо при

                           k  вытекает, что оно справедливо и при  k + 1, значит оно справедливо

                           при любом натуральном  n , что и требовалось доказать.